軸上色収差の考察

軸上色収差は波長毎のレンズの焦点距離の差によって起こる現象だと説明されている
一般の写真用レンズは色消し(アクロマート)レンズで可視光の両端(RB)における周波数帯域で補正を行っている(RBのミックスなのでマゼンタやパープル)
よって、中間のG帯域が残存二次スペクトルとして残る(Gなのでグリーン)
そのようなレンズをモデル化して考察する

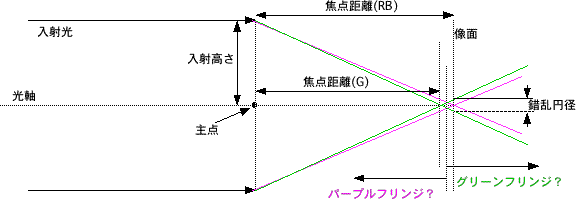
・焦点距離(RB)に主点後方距離(主点<->像面の距離)を合わせた場合、無限遠からの像はグリーンの縁取りを持つ
・焦点距離(G)に主点後方距離を合わせた場合、無限遠からの像はマゼンタやパープルの縁取りを持つ
・有限距離の被写体にフォーカスを合わせる場合(作図は省略する)は通常レンズを繰り出して主点後方距離を増やす
・AFにしろMFにしろ感度の高いのはG帯域なのでフォーカスを合わせたつもりの被写体ではマゼンタやパープルの縁取りとして軸上色収差が目立つと思われる
・RBでのフォーカスを合わせた部分では緑の縁取りが目立つであろう
・前ボケはマゼンタやパープルの縁取りが目立ち、後ろボケはグリーンの縁取りが目立つと思われる
・軸上色収差(図のG成分の「錯乱円径」を考えてみよう)は絞りを絞る(入射高さが低くなる)に従い減少する
図のG成分の「錯乱円径」は入射高さに比例するからである
・軸上色収差は焦点距離が長くなるほど増えることは波長毎の屈折率の違いによるものだと考えれば疑う余地はない
しかし広角レンズ、望遠レンズという観点からは「焦点距離」の長短で判断することは出来ない(像面サイズにより同じ焦点距離でも画角が違うから)
よって、軸上色収差の量は像面サイズに対する比で考察するのが適当である
・同一レンズで比較した場合、像面サイズ(対角長)が長くなると広角レンズであり、短くなると望遠レンズであるので、像面サイズに対する比で考えた場合「軸上色収差は望遠レンズほど多い」と言える
・一般的な許容錯乱円の径は像面対角長の約1/1300程度を採用している
よって、図のG成分の「錯乱円径」の像面対角長からの比がこれ以下であれば軸上色収差は目立たないと言える
また、デジタルカメラのセンサーの場合ピクセルピッチによる比(1/長辺方向の画素数)以下に像面サイズ(長辺の長さ)に対する図のG成分の「錯乱円径」の比が収まればインフォーカスに限って「軸上色収差は現れない」と言って差し支えない
…さらに像面サイズに対する図のG成分の「錯乱円径」の比が小さくなれば、インフォーカスからある程度の範囲内においても「軸上色収差は現れない」…目立たないと言って良いことになる
＊像面が焦点距離(G)の位置にある場合はRB(マゼンタやパープル)成分の「錯乱円径」で考えればよいことになる
・EDレンズやUDレンズ、蛍石などの異常分散の性質を持つ光学素材や、回折光学素子を採用することで残存二次スペクトルによる色収差を低減することが出来る
また、反射式をメインの光学系にすることで色収差を発生させる屈折系の影響を少なくして低減することも出来る
軸上色収差が問題となりやすい望遠レンズには良く採用される設計上のテクノロジーだ

以上、用語に問題があるとかロジックが端折ってあるとか言われるだろうが、わたしはこのように理解している

倍率色収差の考察

倍率色収差は波長毎のレンズの焦点距離の差によって起こる波長毎の像面倍率の差だと説明されている
つまり波長毎に画角が違うと言い換えることが出来る
ということは光軸上で波長毎の主点がずれていること(主点を通過する光線は直進する)で現象を説明できる
そのようなレンズをモデル化して考察する

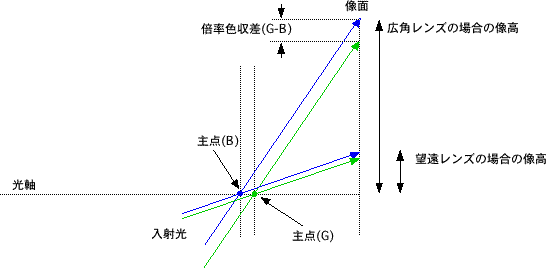
・広角レンズ、望遠レンズという観点からは「焦点距離」の長短で判断することは出来ない(像面サイズにより同じ焦点距離でも画角が違うから)のはすでに述べた
よって、倍率色収差の量も像面サイズに対する比で考察するのが適当である
・同一レンズで比較した場合、像面サイズ(対角長)が長くなると広角レンズであり、短くなると望遠レンズである
・図から明らかなように無限遠からの光線(平行光線)の場合を考察すると広角レンズであろうと望遠レンズであろうと像の端において倍率色収差の像高に対する比は変化しない
・有限距離からの場合は倍率色収差は増える…つまり撮影距離が近くなると目立つことも容易に推察できる
・像面の中心部では倍率色収差は減少する

以上、用語に問題があるとかロジックが端折ってあるとか言われるだろうが、わたしはこのように理解している

軸上色収差と倍率色収差の以上の考察をふまえて「望遠レンズでは軸上色収差が目立ち、倍率色収差は広角レンズの画面の端の方で目立つ」という自身の認識を確認できた

(C)2006.05.02
kuma_san